感度70%の検査で陽性になったということは、70%の確率でその病気に罹患しているということでしょうか?あるいは、特異度99%の検査で陰性になったということは、99%の確率でその病気ではないということでしょうか?実はこれは誤解で、感度・特異度ではその病気に罹患している確率はわかりません。検査結果からその病気に罹患している確率を表すのは陽性適中率という指標になります。
ここでは最近話題になっている新型コロナウイルス感染症を題材にして、検査における感度・特異度と陽性適中率・陰性適中率の関係について説明していきます。
[toc]感度・特異度と陽性適中率・陰性適中率
病気の有無と検査結果で以下のような表を作成します(この表を分割表といいます)。
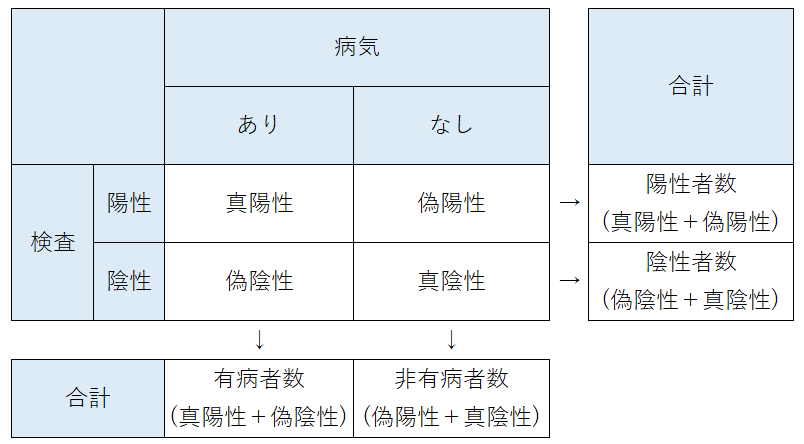
- 真陽性:病気があって検査も陽性の人
- 偽陰性:病気があるのに検査では陰性となってしまった人
- 偽陽性:病気がないのに検査では陽性となってしまった人
- 真陰性:病気がなくて検査も陰性の人
真陽性と真陰性は検査で正しく判定できた人ですが、偽陰性は検査で見逃された人、偽陽性は健康なのに検査で陽性とされた人ということができます。
それでは、この分割表をもとに感度・特異度と陽性適中率・陰性適中率の定義を見ていきましょう。
感度・特異度の定義
- 感度:疾患を有する人のうち、検査陽性を示す人の割合
- 特異度:疾患を有しない人のうち、検査陰性を示す人の割合
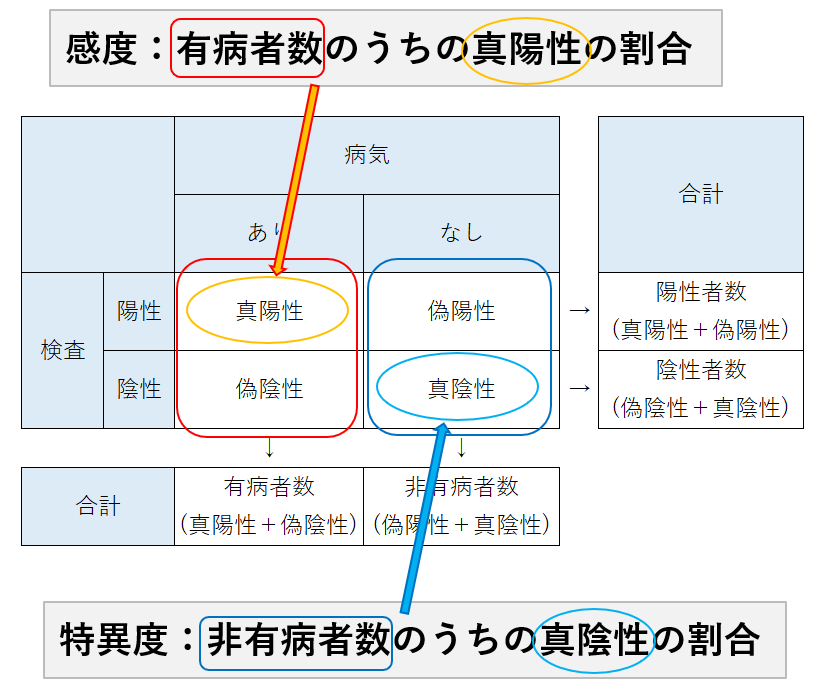
赤で囲まれた有病者数(真陽性+偽陰性)のうち、オレンジの真陽性の人の割合が感度となります。感度が高い検査であれば、病気の人を正しく病気であると判定できることが分かります。
青で囲まれた非有病者数(偽陽性+真陰性)のうち、水色で囲まれた真陰性の割合が特異度となります。特異度が高い検査であれば、病気ではない人を正しく病気ではないと判定できることが分かります。
陽性適中率・陰性適中率の定義
- 陽性適中率:検査陽性者のうち、実際に疾患を有する者の割合
- 陰性適中率:検査陰性者のうち、実際に疾患を有さない者の割合
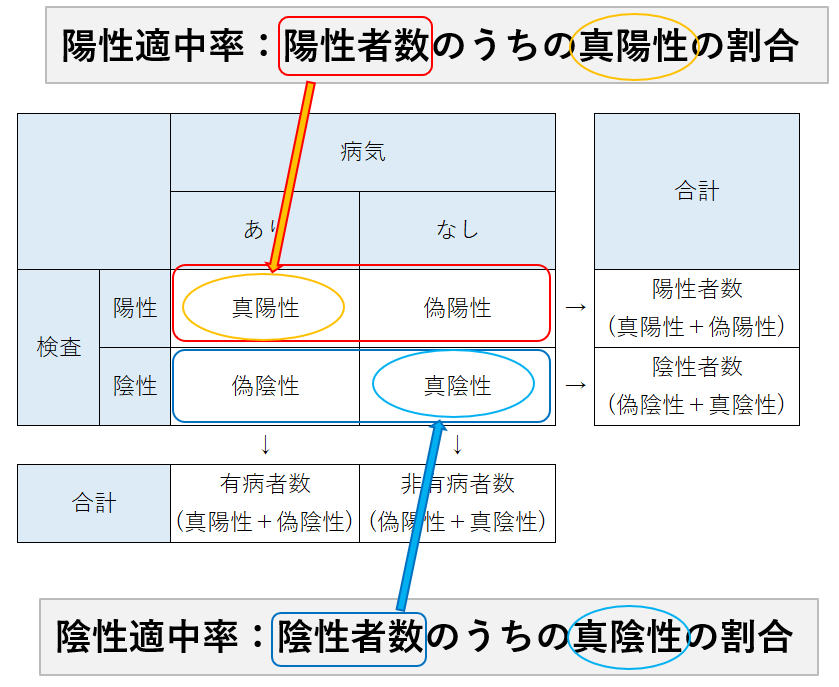
赤で囲まれた陽性者数(真陽性+偽陽性)のうち、オレンジで囲まれた真陽性の割合が陽性適中率です。陽性適中率が高ければ、検査で陽性とされた場合に本当にその病気である可能性が高いといえます。
青で囲まれた陰性者数(偽陰性+真陰性)のうち、水色で囲まれた真陰性の割合が陰性適中率です。陰性適中率が高ければ、検査で陰性とされた場合に本当にその病気ではない可能性が高いといえます。
ここまでの説明で分かる通り、感度・特異度の時と見ているものは同じですが、感度・特異度の時は分割表の縦方向での割合を考えていたのに対して、陽性適中率・陰性適中率は横方向で比較しているという違いがあります。
結局何を知りたい?
では、何かの検査を受けて陽性もしくは陰性の結果を受け取ったときに、実際に知りたい情報は何でしょうか?それは、「検査結果は〇〇だったが、本当のところはどうなのか?」ということですよね。つまり、例えば「検査で陽性であれば何%の確率でその病気であるのか?」ということです。これを表す指標こそが、陽性適中率と陰性適中率なのです。
感度や特異度は、「検査結果が陽性であった人が本当にその病気である確率」を表す指標ではないことに注意してください。
でも、実際にその検査について調べると感度や特異度の情報はあっても陽性適中率と陰性適中率の情報は出てきませんよね?なぜでしょうか?それは、感度や特異度はその検査固有の値ですが、陽性適中率と陰性適中率はその病気の有病率によって変化する値だからです。
感度・特異度と陽性適中率・陰性的中率の関係
例えば、感度70%、特異度99%の検査を考えてみます。この検査を有病率10%の疾患に対して行ったとします。すると以下のようになって、陽性適中率・陰性適中率ともにかなり高い値になっていることが分かります。
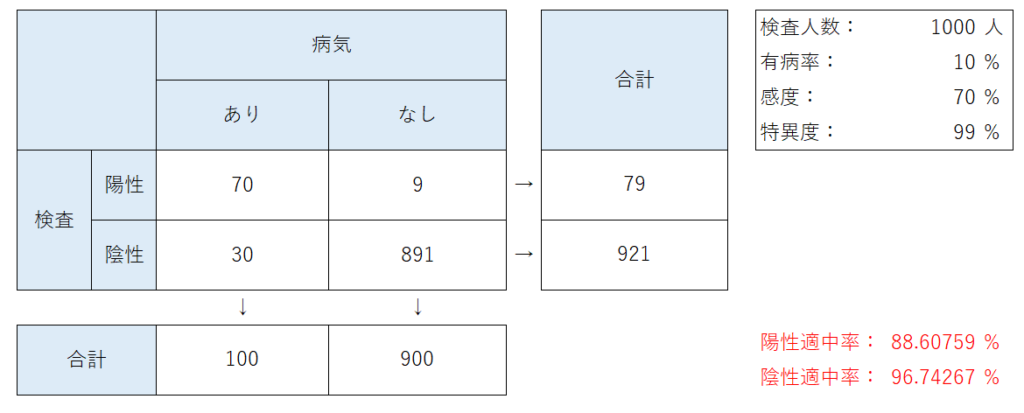
それでは、同じ感度・特異度の検査を有病率1%の疾患に対して行ってみましょう。すると、以下のようになり、陽性適中率が41.42%にまで下がってしまっています。
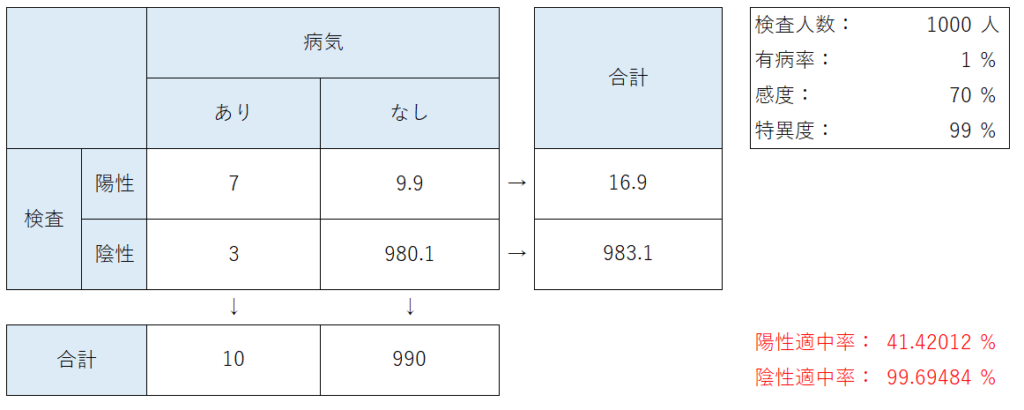
つまり、有病率が10%の時は、その検査で陽性であれば88.61%の確率でその病気であると診断できたのに、有病率が1%になると同じ検査で陽性の結果が出ても41.42%の確率でしかその病気であると言えなくなってしまいます。
このように陽性適中率・陰性適中率は有病率の影響を大きく受けることが分かります。
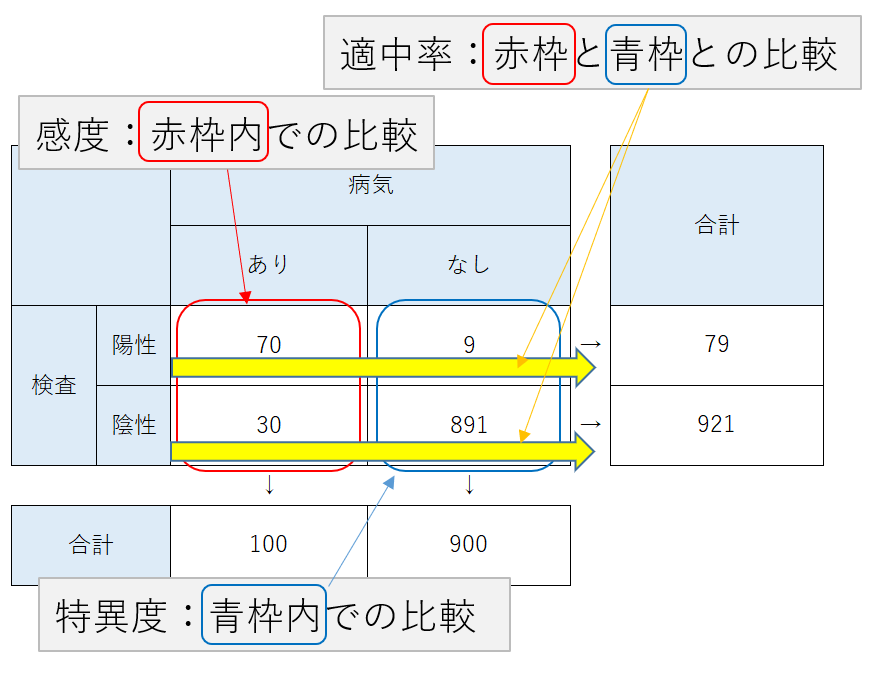
なぜこのようになるかという理由は次の通りです。感度は上図の赤枠内での人数の比較、特異度は上図の青枠内での人数の比較ですが、陽性適中率・陰性適中率は赤枠と青枠の人数の比較になります。そして、赤枠と青枠の比を決めるのが有病率だからです。
例えば、特異度が非常に高くて偽陽性が非常に少ない検査であっても、有病率が低くて「病気なし」の人が多くなると、偽陽性の人の絶対数は大きくなります。同時に「病気あり」の人数が減るので、真陽性の人の絶対数は少なくなります。つまり、相対的に偽陽性が増えるので、陽性適中率が小さくなってしまうという訳です。
陽性適中率と陰性適中率の計算方法
感度・特異度と有病率から陽性適中率・陰性適中率が計算可能と言いましたが、どのようにして求めればよいでしょうか?分割表を書けば簡単に求めることはできるのですが、数式で書ければより理解が深まりますので、ここでは数式で考えていきましょう。なお、数学が苦手な方はここでの説明は飛ばしてしまっても大丈夫です。
陽性適中率と感度・特異度・有病率の関係
陽性適中率は条件付確率を用いて \( P(疾患あり|検査陽性) \)と書けます。
ベイズの定理から
$$
P(疾患あり|検査陽性) = \frac{P(検査陽性|疾患あり) P(疾患あり)} {P(検査陽性)}
$$
ここで、
$$
\begin{cases}
P(検査陽性|疾患あり) = 感度\\
P(疾患あり) = 有病率\\
\begin{align}
P(検査陽性) &= P(検査陽性|疾患あり) P(疾患あり) + P(検査陽性|疾患なし) P(疾患なし) \\
& = 感度 \times 有病率 + (1 – 特異度) \times (1 – 有病率)
\end{align}
\end{cases}
$$
となることから、陽性適中率は
$$
P(疾患あり|検査陽性)=\frac{感度 \times 有病率}{感度 \times 有病率 + (1 – 特異度) \times (1 – 有病率)}
$$
となります。
この式から、陽性適中率は感度・特異度・有病率によって定まることが分かります。さらに、非常に有病率が低い疾患である場合は、\( 感度 \times 有病率 \)が小さくなるので、特異度が高くないと分母の\( (1 – 特異度) \times (1 – 有病率) \)の部分の影響が強く出てしまい、陽性適中率が低い値になってしまうことが分かります。
それでは次に陽性適中率と有病率の関係を求めてみましょう。なお細かい計算式は分からなくても、結論だけ理解していれば十分です。
有病率を\( x \)、陽性適中率を\( y \)として、\( x \)と\( y \)の関係を求めてみます。ここで、感度を\( A \)、特異度を\( 1-B \)とおくと、
$$
\begin{align}
y&=\frac{Ax}{Ax+B(1-x)}\\
&=\frac{Ax}{(A-B)x+B}
\end{align}
$$
となり、これを変形すると、
$$
(x+\frac{B}{A-B})(y-\frac{A}{A-B})=-\frac{AB}{(A-B)^2}
$$
となり、有病率\( x \)と陽性適中率\( y \)は反比例の関係があることが分かります。例えば、感度70%、特異度99%の検査の場合は、有病率\(x\)と陰性適中率\(y\)の関係は以下のようなグラフになります。
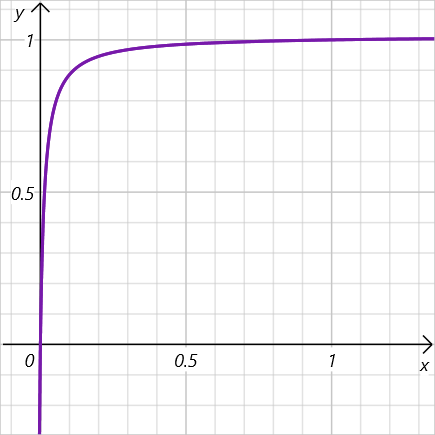
このグラフから、有病率\( x \)が0に近づくと、陽性適中率が急激に減少することが分かります。
陰性適中率と感度・特異度・有病率の関係
陽性適中率の場合と同様に、陰性適中率を感度・特異度・有病率から求めてみましょう。陰性適中率は条件付確率を用いて \( P(疾患なし|検査陰性) \)と書けます。
ベイズの定理から
$$
P(疾患なし|検査陰性) = \frac{P(検査陰性|疾患なし) P(疾患なし)} {P(検査陰性)}
$$
ここで、
$$
\begin{cases}
P(検査陰性|疾患なし) = 特異度\\
P(疾患なし) = 1-有病率\\
\begin{align}
P(検査陰性) &= P(検査陰性|疾患なし) P(疾患なし) + P(検査陰性|疾患あり) P(疾患あり) \\
& = 特異度 \times (1-有病率) + (1 – 感度) \times 有病率
\end{align}
\end{cases}
$$
となることから、陰性適中率は
$$
P(疾患なし|検査陰性)=\frac{特異度 \times (1-有病率)}{特異度 \times (1-有病率) + (1 – 感度) \times 有病率}
$$
となります。
この式から、陰性適中率も感度・特異度・有病率によって定まることが分かります。さらに、有病率が高い疾患である場合は、\( 特異度 \times (1-有病率) \)が小さくなるので、感度が高くないと分母の\( (1 – 感度) \times 有病率 \)の部分の影響が強く出てしまい、陰性適中率が低い値になってしまうことが分かります。
では、有病率を\( x \)、陰性適中率を\(y\)として、先ほどと同様に\(x\)と\(y\)の関係を求めてみます。ここで、特異度を\(C\)、感度を\(1−D\)とおくと、
$$
\begin{align}
y=\frac{C(1-x)}{C(1-x) + Dx}
\end{align}
$$
となります。この式を変形すると
$$
(x-\frac{C}{C-D})(y-\frac{C}{C-D})=\frac{CD}{(C-D)^2}
$$
となり、先ほどと同様に有病率\(x\)と陰性適中率\(y\)との間には反比例の関係があることが分かります。例えば、感度70%、特異度99%の検査の場合は、有病率\(x\)と陰性適中率\(y\)との関係は以下のようなグラフになります。
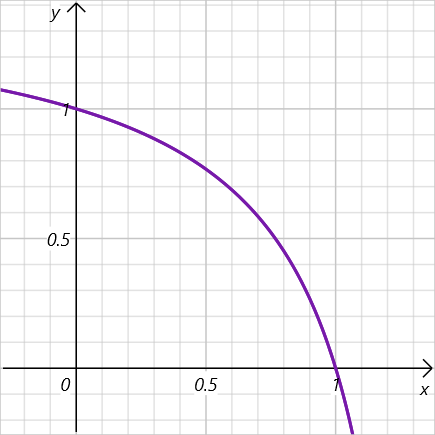
このグラフより、有病率\(x\)が上昇するにしたがって陰性適中度\(y\)が減少していることが分かります。
実際に陽性適中率と陰性適中率を計算してみましょう!
では、最後に陽性適中率と陰性適中率を自分でも計算してみましょう。上記で使用した陽性適中率・陰性適中率を計算するExcelシートは以下に載せておきましたので、ダウンロードしてお使いください。
また、以下のサイトには感度・特異度・適中率の計算をブラウザ上から実行できるWebアプリが公開されています。
ブラウザ上で有病率・感度・特異度を指定するだけで陽性適中率・陰性適中率を簡単に計算することができます。
なお、アプリ公開元のWebsiteは以下です。
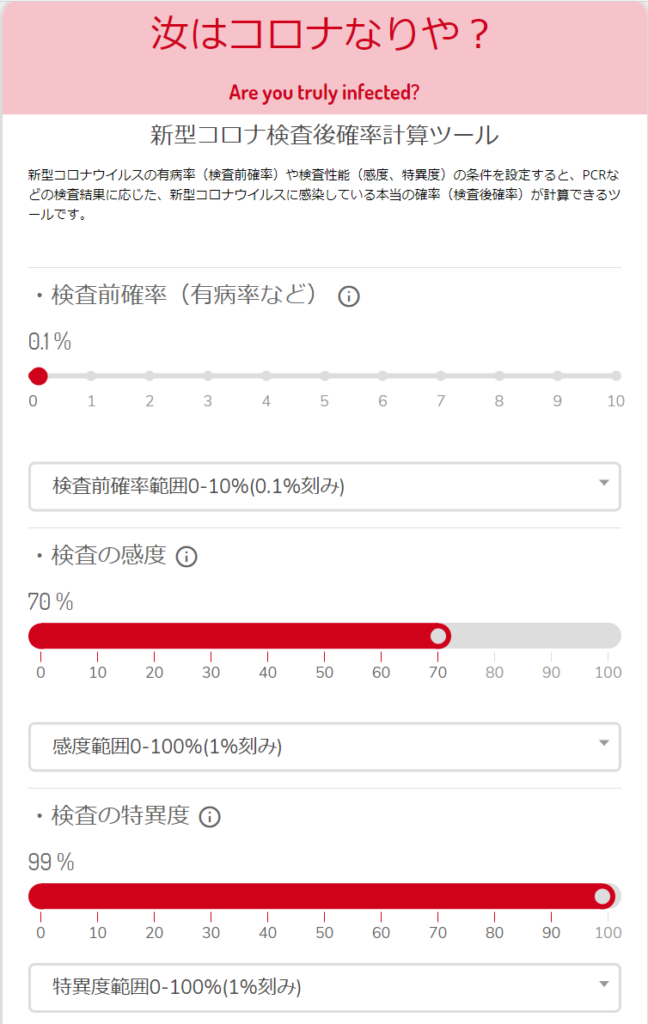
ちなみに、検査前確率・検査後確率という用語もありますが、検査前確率=有病率、検査後確率=陽性適中率と読み替えてしまって問題ありません。(もちろん、検査前確率は誰を対象とした検査かによって変わってきます)
これらのツールを活用して感度・特異度・有病率と陽性適中率・陰性適中率についてイメージをつけてみましょう。








コメント