確率からオッズやロジットといった様々な概念が生み出されています。それらを活用することで医療統計の分野などでおなじみのロジスティック回帰モデルも説明できます。でも、オッズやロジットとロジスティック回帰モデルの関係を理解できていますか?そもそも、ロジスティック回帰モデルの「ロジスティック」ってどういう意味ですか?
ここではそれらの疑問を解いていきましょう!

確率とオッズ・ロジット
確率pに対して、その事象が起こる確率を起こらない確率で割った値をオッズ(odds)、オッズの対数をロジット(logit)と呼びます。
それぞれ
$$odds=\frac{p}{1-p}$$
$$logit=log(\frac{p}{1-p})$$
で定義され、確率とオッズ、ロジットは相互に変換可能です。
確率からオッズやロジットを考えることで以下のように様々な概念に拡張することができます。
オッズから拡張できる概念
オッズ比 ― 相対危険度の計算に有用
2つのオッズ(odds1、odds2)の比 \( \displaystyle \frac{odds1}{odds2}\)をオッズ比といいます。このオッズ比はケースコントロール研究において相対危険度(その要因によって疾患の発生率が何倍になるかを表す数値)を近似する値として非常に重要です。
例えば、以下のようなケースコントロール研究の結果を考えてみましょう。
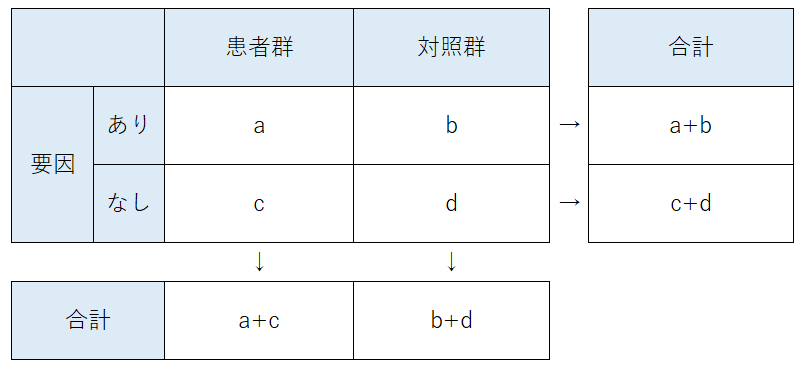
ここで、ケースコントロール研究における患者群と対照群の割合は実際の罹患率を反映しているわけではなく恣意的に決めたものなので、患者群と対照群の人数から実際の罹患率を反映できるように\(k\)を定義します。
$$(実際の病気ありの人数) : (実際の病気なしの人数) = k \times (患者群の人数) : (対照群の人数)$$
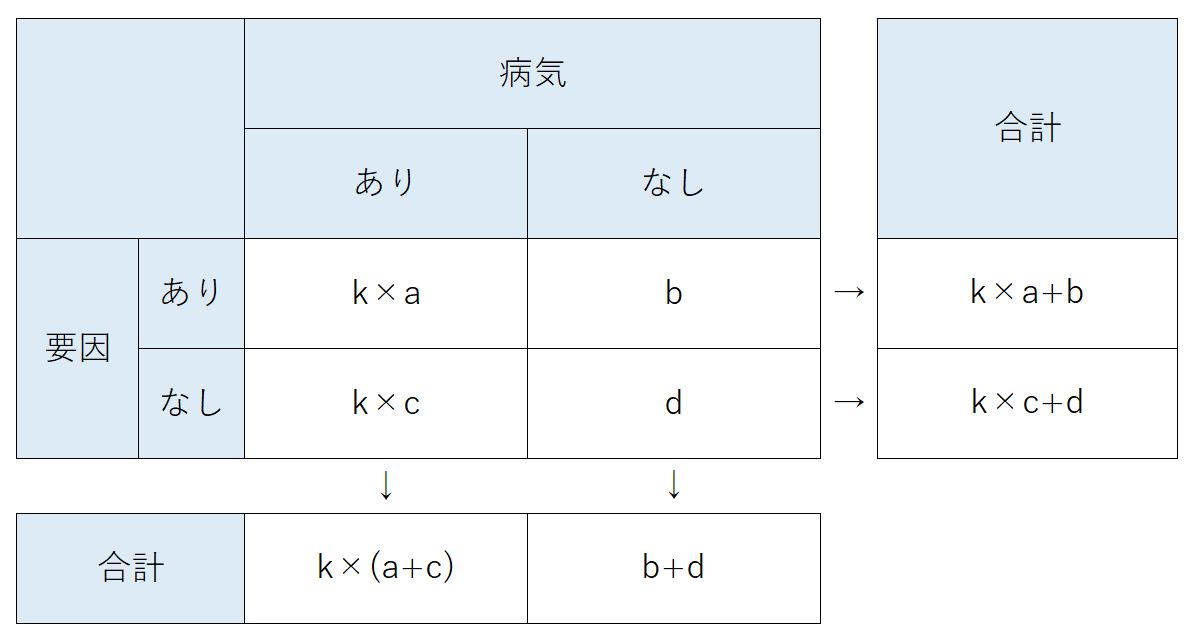
相対危険度は
$$相対危険度=\frac{要因ありの罹患率}{要因なしの罹患率}=\frac{ka / (ka+b)}{kc / (kc+d)}=\frac{a (kc+d)}{c (ka+b)}$$
ここで母集団における罹患率が十分小さい時(対象とする疾病の発生率が数パーセント以下の時)は、\( k \approx 0 \)として
$$\frac{kc+d}{ka+b}\approx\frac{d}{b}$$
と近似できるので、
$$相対危険度=\frac{a (kc+d)}{c (ka+b)} \approx \frac{ad}{cb}$$
と近似できます。
要因ありのオッズは\( \displaystyle \frac{ka}{b} \)、要因なしのオッズは\( \displaystyle \frac{kc}{d} \)なので、オッズ比は
$$オッズ比=\frac{ka / b}{kc / d}=\frac{ad}{cb}$$
となります。
以上より、
$$相対危険度 \approx \frac{ad}{cb}=オッズ比$$
と近似することができました。
ケースコントロール研究においては、相対危険度を直接計算することはできないので、オッズ比を用いて近似できることが重要です。
ロジットから拡張できる概念
ロジット関数と標準ロジスティック関数
ロジットを確率pの関数だとみなしたときに、これをロジット関数と呼びます。
ロジット関数logit(p)は
$$logit(p)=log(\frac{p}{1-p})$$
ロジット関数の逆関数が標準ロジスティック関数となり、
$$p=\frac{1}{1+e^{-x}} (ただし、x=logit(p))$$
と表されます。
この関数\( \displaystyle f(x)=\frac{1}{1+e^{-x}}\)で表される曲線は標準シグモイド曲線とも呼ばれています。
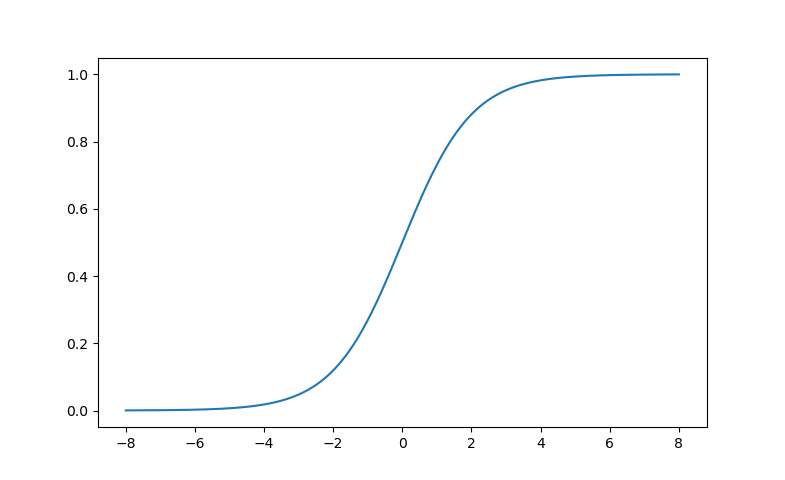
このグラフの形からも分かる通り、標準ロジスティック関数は単調増加関数でありながらその値は0から1の範囲に収まっているのが最大の特徴です。つまり、標準ロジスティック関数はどんな値を与えても0から1の間の一意の数に変換してくれるので、「標準ロジスティック関数は任意の数を確率に変換する関数」だと考えることができます。
ロジスティック回帰モデル
ロジスティック回帰モデルは「あり・なし」「生・死」のようにある事象が起こるか起こらないかの離散的な2つの値から成る目的変数を、連続的な説明変数で表すときに用いるモデルです。実際にはロジスティック回帰モデルの目的変数は、その事象が起こる確率で表されます。医療統計では「生・死」が目的変数となることが多いので、ロジスティック回帰モデルは非常におなじみのものですね。
数学的には一般化線形モデルのリンク関数にロジット関数を用いたものがロジスティック回帰モデルになります。
ロジスティック回帰モデル
説明変数を\(x_1, x_2, x_3, … ,x_n\)、目的変数を\(p\)(その事象が起こる確率)としてロジスティック回帰モデルを具体的に見てみましょう。
まず説明変数\(x_1, x_2, x_3, … ,x_n\)に対して、
$$logit(p)=a_1*x_1+a_2*x_2+a_3*x_3+…+a_n*x_n+b$$
というように、説明変数と回帰係数\(a_1, a_2, …, a_n\)の1次結合で\(logit(p)\)を表します。
これを\(p\)について解くと、標準ロジスティック関数で表せるので、
$$p=\frac{1}{1+e^{-(a_1*x_1+a_2*x_2+a_3*x_3+…+a_n*x_n+b)}}$$
となり、説明変数\(x_1, x_2, x_3, … ,x_n\)によって目的変数\(p\)(その事象が起こる確率)が表されていることが分かります。これがロジスティック回帰モデルです。
実際のロジスティック回帰分析では、ここで作成したロジスティック回帰モデルの式から、実際のデータを最もよく説明するような回帰係数を最尤法を用いて推定します。
回帰係数の統計的解釈(説明変数のオッズ比)
先ほどのロジスティック回帰モデルのロジットの式から
$$logit(p)=a_1*x_1+a_2*x_2+…+a_n*x_n+b$$
$$\frac{p}{1-p}=e^{a_1*x_1+a_2*x_2+…+a_n*x_n+b}=e^{a_1*x_1}*e^{a_2*x_2}*…e^{a_n*x_n}*e^b$$
となり、着目している事象のオッズと説明変数との関係が導けます。
それでは、回帰係数\(a_1\)が目的変数に与える影響を考えてみましょう。回帰係数\(a_1\)に対応する説明変数\(x_1\)を0から1に変化させて、それ以外の説明変数は全く同じにしたときのオッズは以下のようになります。
$$x_1=0の時:odds_0=\frac{p_0}{1-p_0}=e^{a_1*0}*e^{a_2*x_2}*…e^{a_n*x_n}*e^b$$
$$x_1=1の時:odds_1=\frac{p_1}{1-p_1}=e^{a_1*1}*e^{a_2*x_2}*…e^{a_n*x_n}*e^b$$
つまり、\(x_1=0\)の場合に対する\(x_1=1\)の場合のオッズ比は
$$\frac{odds_1}{odds_0}=e^{a_1}$$
\(x_1=0\)の場合を「要因なし」、\(x_1=1\)の場合を「要因あり」とすると、ケースコントロール研究の場合と同様に考えることができるので、このオッズ比がその説明変数の相対危険度だと言えます。(着目している事象の母集団における発生率は十分小さいと仮定しています)
おまけ:ロジスティック関数の本来の意味
今まで確率からオッズやロジットを定義してロジスティック関数にまで概念を広げて、ロジスティック回帰モデルを説明してきました。しかし、実はこのロジスティック関数は本来は確率論や統計学における関数ではありません。ロジスティック回帰モデルが発表されるはるか以前から数理生物学の分野でロジスティック関数が導入されていて、たまたま確率論から発展させた関数も同じ関数になっただけのことです。
ロジスティック関数はもともとは数理生物学の生態系系シミュレーションにおける「ロジスティック成長モデル」がもとになっています。ロジスティック成長モデルは生物の個体数増殖のモデルで、次のようなロジスティック方程式を考えます。
$$\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right)$$
ただし、\(N\):個体数、\(t\):時間、\(r\):内的自然増加率、\(K\):環境収容力とします。
この微分方程式の解がロジスティック関数です。
$$N=\frac{K}{1+(K / N_0-1)e^{-rt}}$$
このロジスティック関数の特殊なものが先ほど説明した標準ロジスティック関数\(f(x)\)となります。
$$f(x)=\frac{1}{1+e^{-x}}$$
ちなみに先ほどのロジスティック回帰モデルが発表されたのは1958年のことですが、ロジスティック方程式は1838年に発案されたものです。つまり、ロジスティック関数は統計モデルで知られるよりもはるか以前から数理モデルでは有名な関数だったのです。確率論の概念から発展させた関数が、たまたま他の分野の微分方程式の解と同じ関数になっていたというのはとても興味深いことですね。(もっとも、すでにあるロジスティック関数に合わせて確率論の概念を拡張したという方が正確かもしれませんが)
なお、ロジスティック方程式の「ロジスティック」という名前は1845年のフェルフルストによる論文で与えられていますが、その名前の由来には言及されておらず不明だそうです。








コメント