データ解析において、標本値から近似曲線を作成することや、そこで求めた近似曲線(モデル式)がどの程度当てはまっているかを示す決定係数(\(R^2\))を求めることは必須の技術です。Excelを使えば非常に簡単に近似曲線と決定係数(\(R^2\))を求めることできますが、Pythonを使う場合はどのようにすればよいのでしょうか。Pythonでは近似曲線を求めるための方法がいくつか用意されており、さらに決定係数(\(R^2\))を求めるためには近似曲線とは別のモジュールを用いる必要があるので、やや分かりにくくなっています。
ここでは、Pythonを用いた近似曲線・決定係数(\(R^2\))の求め方を説明していきます。
開発環境
- matplotlib 3.1.3
- NumPy 1.18.1
- Pandas 1.0.3
- Python 3.7.7
- scikit-learn 0.22.1
- SciPy 1.4.1

準備
実際のシチュエーションを想定して、Excelに入力したデータから近似曲線や決定係数(\(R^2\))を求めていきます。
ExcelからDataFrameとしてデータを取得する方法は以下の記事をご覧ください。

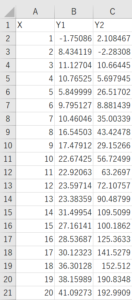
ここでは次のサンプルデータを用いて近似曲線と決定係数を求める方法を見ていきます。
(サンプルデータは以下から.xlsx形式でダウンロード可能です)
サンプルデータのY1、Y2はそれぞれ次のようなデータになります。
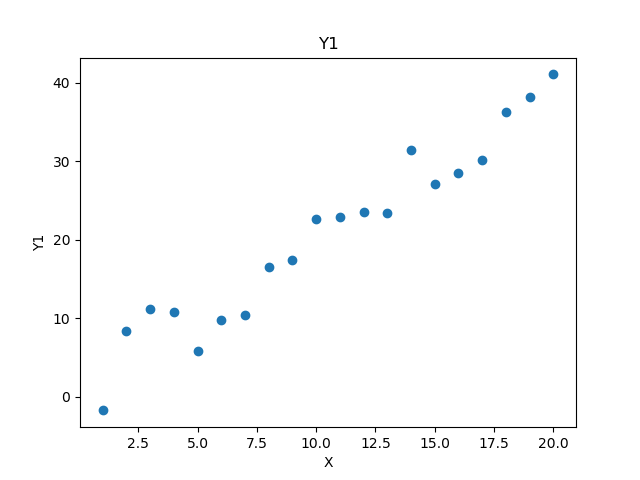
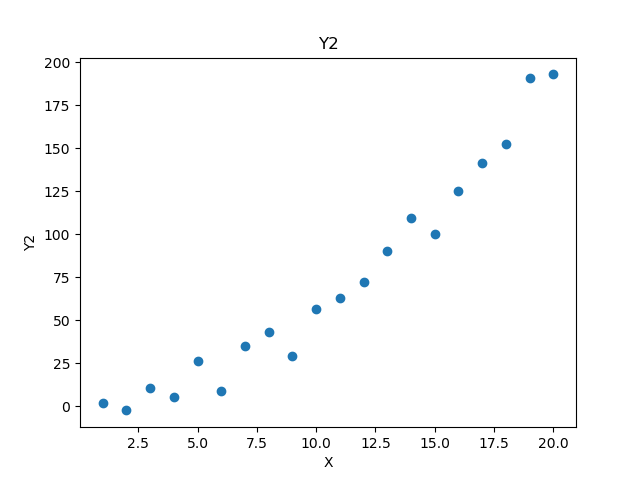
近似曲線を求める
近似曲線を求める方法は以下の3通りがあります。
近似曲線(多項式近似)の係数を指定して求める
NumPyのpolyfit関数を用いて、多項式の次数を指定するだけで簡単に多項式近似することができます。polyfit関数の第3引数に次数を指定すれば、データにフィットする多項式の係数をリストで取得できます。
例えば、サンプルのY1を1次関数で近似してみましょう。
# データの読み込み
import pandas as pd
df = pd.read_excel('https://biotech-lab.org/wp-content/uploads/2020/08/4907-Sample-01.xlsx')
# 一次関数で多項式近似を行う
import numpy.polynomial.polynomial as P
coef = P.polyfit(df['X'], df['Y1'], 1)
# 作成した多項式近似を表示
print('y = ' + str(coef[0]) + ' + ' + str(coef[1]) + ' * x')
y = 0.5402729723647073 + 1.9207160692921308 * x
ここで求めた近似関数は、求めた係数をpolyval関数に渡すことで求めることができます。これを用いて近似曲線も描いてみましょう。先ほどのコードの続きです。
# 作成した近似曲線の(x, y)の組み合わせを求める
import numpy as np
x = np.arange(0, 20, 0.1)
y = P.polyval(x, coef)
# 元データと近似曲線をプロット
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(df['X'], df['Y1'])
ax.plot(x, y)
ax.set_xlabel('X')
ax.set_ylabel('Y1')
ax.set_title('Y1')
plt.show()
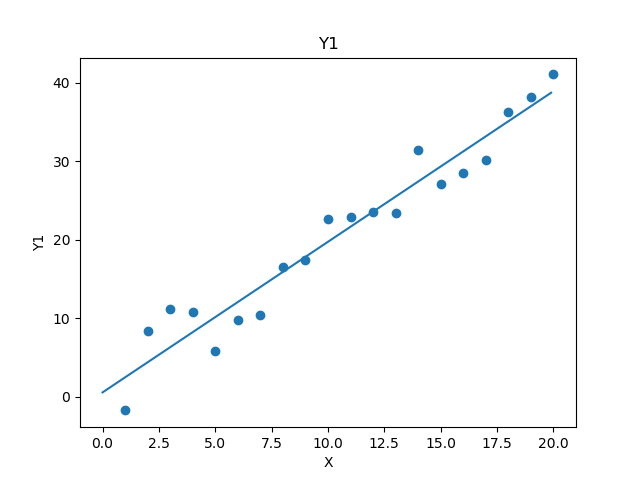
同様にサンプルのY2を2次関数で近似する場合は
# データの読み込み
import pandas as pd
df = pd.read_excel('https://biotech-lab.org/wp-content/uploads/2020/08/4907-Sample-01.xlsx')
# 二次関数で多項式近似を行う
import numpy.polynomial.polynomial as P
coef = P.polyfit(df['X'], df['Y2'], 2)
# 作成した多項式近似を表示
print('y = ' + str(coef[0]) + ' + ' + str(coef[1]) + ' * x + ' + str(coef[2]) + ' * x^2')
とすることで、以下のように近似関数を求めることができます。
y = 0.10764257318310382 + 0.7440469214788494 * x + 0.4516653709746952 * x^2
このように多項式の次数を指定するだけで簡単に近似関数を求めることができる方法なのですが、しかし、例えば「原点を通る近似曲線を描く」などの指定はできません。そのような場合は、次の方法を用いましょう。
近似曲線の関数を指定して求める
1次関数に近似する
SciPyのcurve_fit関数を用いることで、データ系列を任意の関数に近似させることができます。
# データの読み込み
import pandas as pd
df = pd.read_excel('https://biotech-lab.org/wp-content/uploads/2020/08/4907-Sample-01.xlsx')
# 近似させる関数の定義
def func(x, a, b):
return a + b*x
# 近似関数を求める
import scipy.optimize as optimize
popt, _ = optimize.curve_fit(func, df['X'], df['Y1'])
print(popt)
[0.54027297 1.92071607]
ここで求めた近似曲線に値を代入してみるときは、次のように最初に定義した関数にcurve_fitで求めた値を展開して渡します。これを用いて近似曲線も描いてみましょう。先ほどのコードの続きです。
# 作成した近似曲線の(x, y)の組み合わせを求める
import numpy as np
x = np.arange(0, 20, 0.1)
y = func(x, *popt)
# 元データと近似曲線をプロット
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.scatter(df['X'], df['Y1'])
ax.plot(x, y)
ax.set_xlabel('X')
ax.set_ylabel('Y1')
ax.set_title('Y1')
plt.show()
※ y = func(x, *popt) のようにリスト名に*を付けて引数に指定すると、リストを展開して引数に渡してくれます。

原点を通る1次関数に近似する
SciPyのcurve_fit関数を用いると、任意の関数に近似できるので、例えば上の例を原点を通るに近似させることもできます。
# データの読み込み
import pandas as pd
df = pd.read_excel('https://biotech-lab.org/wp-content/uploads/2020/08/4907-Sample-01.xlsx')
# 近似させる関数の定義
def func(x, a):
return a*x
# 近似関数を求める
import scipy.optimize as optimize
popt, _ = optimize.curve_fit(func, df['X'], df['Y1'])
print(popt)
[1.96024824]
おまけ ― least_squares関数を用いる方法
なお、SciPyのleast_squares関数を用いて任意の多項式関数に近似する方法もありますが、curve_fit関数の方が万能ですし、least_squares関数は使い方に若干癖があるので、ここでは細かい説明は省略します。
サンプルのY1を1次関数で近似するコードをお示しします。
# データの読み込み
import pandas as pd
df = pd.read_excel('https://biotech-lab.org/wp-content/uploads/2020/08/4907-Sample-01.xlsx')
# 近似させる関数の定義
def func(param,x,y):
residual = y - (param[0]*x + param[1])
return residual
# 近似関数を求める
import scipy.optimize as optimize
res_least = optimize.least_squares(func, [0,0], args=(df['X'], df['Y1']))
print(res_least)
active_mask: array([0., 0.])
cost: 80.300382627718
fun: array([-4.21184572, 4.0524143 , 4.82462042, 2.54211517, -4.29385436,
-2.26944209, -3.52482768, 0.6390253 , -0.34759802, 2.92681136,
1.2524811 , 0.00827313, -2.12598704, 4.06923905, -2.18960598,
-2.7348631 , -3.06921655, 1.18811313, 1.12601341, 2.13813417])
grad: array([8.39149180e-07, 1.77635684e-14])
jac: array([[ -1.00000002, -1. ],
[ -2. , -1. ],
[ -2.99999998, -1. ],
[ -4. , -1. ],
[ -4.99999998, -1. ],
[ -5.99999997, -1. ],
[ -7.00000002, -1. ],
[ -8. , -1. ],
[ -8.99999998, -1. ],
[ -9.99999997, -1. ],
[-11.00000008, -1. ],
[-11.99999994, -1. ],
[-12.99999992, -1. ],
[-14.00000003, -1. ],
[-15.00000002, -1. ],
[-16. , -1. ],
[-17.00000011, -1. ],
[-17.99999997, -1. ],
[-19.00000008, -1. ],
[-19.99999994, -1. ]])
message: 'Both `ftol` and `xtol` termination conditions are satisfied.'
nfev: 4
njev: 4
optimality: 8.391491803649842e-07
status: 4
success: True
まとめ – どの関数を使えばいい?
シンプルに1次近似、2次近似を行うのであれば、NumPyのpolyfit関数を使うのが一番簡単です。ただし、この方法では例えば「原点を通る」ように指定をするといった細かい指定ができません。その場合はSciPyのcurve_fit関数を用いる必要があります。least_squares関数を用いて近似することもできますが、curve_fit関数の方が汎用性があって使い方も素直なので、個人的にはこちらの方がお勧めです。
決定係数(\(R^2\))を求める
sklearnのr2_score関数を用いることで、決定係数(\(R^2\))を求めることができます。サンプルデータのY2を2次関数で近似し、その決定係数(\(R^2\))を求めてみましょう。
# データの読み込み
import pandas as pd
df = pd.read_excel('https://biotech-lab.org/wp-content/uploads/2020/08/4907-Sample-01.xlsx')
# 近似させる関数の定義
def func(x, a, b, c):
return a * x**2 + b * x + c
# 近似関数を求める
import scipy.optimize as optimize
popt, _ = optimize.curve_fit(func, df['X'], df['Y2'])
# 近似関数の決定係数(R2)を求める
import sklearn.metrics as metrics
r2 = metrics.r2_score(df['Y2'], func(df['X'], *popt))
print(r2)
0.983348860455
r2_score関数の第1引数に実際のデータを、第2引数に近似関数からの予測値を指定します。なお、r2_score関数の引数にはSeriesをそのまま渡すことができます。









コメント