生存時間解析の大きな目的の一つは、「ある治療によってその患者の生存が改善するかどうか」を明らかにすることです。そのような解析のためには2群の生存確率関数の差の検定を行う必要があり、その方法の1つとしてログランク検定や一般化Wilcoxon検定が知られています。ここではPythonを用いてログランク検定や一般化Wilcoxon検定を行う方法を説明します。
開発環境
- lifelines 0.26.3
- Python 3.7.11

ログランク検定・一般化Wilcoxon検定とは?
ログランク検定・一般化Wilcoxon検定の概要
生存時間解析では、まずカプラン・マイヤー曲線を描いてデータを可視化します。
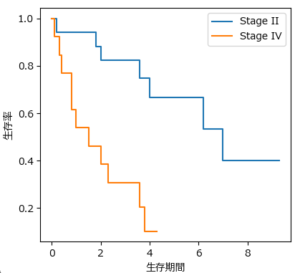
ここである癌のステージ別の生存率が次のように取得できたとします。このグラフからは明らかにStage II(青)の方がStage IV(オレンジ)のものよりも生存率が高そうですが、それを統計的に証明するにはどうすればよいのでしょうか?この時に登場するのがログランク検定や一般化Wilcoxon検定です。これにより2群の生存確率関数に統計的な差(有意差)があるのかどうかを検定することが可能になります。
なお、カプラン・マイヤー推定量と生存率曲線については以下の記事をご覧ください。
ログランク検定・一般化Wilcoxon検定の数学的背景
ログランク検定と一般化Wilcoxon検定はともに同じ考え方の検定方法で、その違いは統計量の算出方法に標本サイズの重みをつけるかどうかです。両者の帰無仮説と対立仮説は次のようになります。
- 帰無仮説:両群の生存確率関数に差がない
- 対立仮説:両郡の生存確率関数に差がある
生存確率関数は一度きりのイベントの累積発生確率についての関数ですが、生存/死亡について見る場合は、次のように言い換えることができます。
- 帰無仮説:すべての死亡イベント発生時点で、2群の生存率は等しい
- 対立仮説:ある死亡イベント発生時点においては、2群の生存率に差がある
この仮説を検定するために、まずは任意の死亡時刻 \(t_{i}\) における2群(A群/B群)の死亡個体数・生存個体数の2×2分割表を考えます。
| 死亡時刻 \(t_{i}\) | \(t_{i}\) における死亡個体数 | \(t_{i}\) を超える生存個体数 | \(t_{i}\) 直前での生存個体数 |
|---|---|---|---|
| A群 | \(d_{Ai}\) | \(n_{Ai}-d_{Ai}\) | \(n_{Ai}\) |
| B群 | \(d_{Bi}\) | \(n_{Bi}-d_{Bi}\) | \(n_{Bi}\) |
| 計 | \(d_i\) | \(n_i-d_i\) | \(n_i\) |
すべての死亡時刻(打ち切り時刻を除く)で上記のような分割表を書くことができます。
この分割表における次の周辺度数
- その死亡時刻\(t_i\)における合計の死亡個体数(\(d_i\))
- 生存個体数(\(n_i-d_i\))
- \(t_i\)直前でのA群・B群の生存個体数(\(n_{Ai}\)・\(n_{Bi}\))
- 上記の合計(\(n_i\)))
は分かっているので、あとは内部の4つのセルのどれかが決まればすべて決まります。ここでは左上の\(d_{Ai}\)に注目してみましょう。時刻\(t_i\)における観測度数\(o_i\)について、ここでは\(o_i=d_{Ai}\)とします。この時の期待度数を\(e_i\)とすると、A群とB群との生存確率関数に差がなければ\(o_i=e_i\)となりますが、差があると\(o_i\)と\(e_i\)の値が大きく異なります。つまり、すべての死亡イベントが発生した時刻における\(o_i\)と\(e_i\)の差を足し合わせた統計量を考えればA群とB群に差があるかどうかを判断する材料とすることができると言えます。
そこで、時刻\(t_i\) (\(i=1,…,r\))における観測度数\(o_i\)の期待度数\(e_i\)と分散\(v_i\)を用いて、ログランク統計量\(\chi^2_L\)と一般化Wilcoxon統計量\(\chi^2_W\)を次のように定義します。
$$ログランク統計量 \ \chi^2_L=\frac{{\left\{ \displaystyle \sum_{i=1}^{r}{(o_i-e_i)}\right\}}^2}{\displaystyle \sum_{i=1}^{r}v_i}$$
$$一般化Wilcoxon統計量 \ \chi^2_W=\frac{{\left\{ \displaystyle \sum_{i=1}^{r}{n_i(o_i-e_i)}\right\}}^2}{\displaystyle \sum_{i=1}^{r}{n_i^2v_i}}$$
これはともに\(\chi^2\)分布に従うことが知られており、これを用いた検定がそれぞれログランク検定と一般化Wilcoxon検定です。基本的な考え方は分割表の適合度を検定するカイ二乗検定と類似したものになります。
一般的にカプラン・マイヤー曲線では、最初は標本数が多いので信頼できる生存率が出ていますが、時間が経つにつれて死亡や脱落が増えて、標本数が減るので信頼できる生存率とは言えなくなってきます。このことを補正するために一般化Wilcoxon統計量ではイベント直前の生存数で重みづけられているのです。一般化Wilcoxon検定では標本数の多い時間経過の早い時点でのデータを重視して扱うので、「時間経過が早い時点では生存率に差が出ているが、徐々に生存率が同じになる」ようなケースでは有意差が付きやすくなるという特徴があります。
なお、ログランク検定と一般化Wilcoxon検定はともに生存確率関数について特定の分布を仮定する必要のないノンパラメトリックな検定手法となります。
Pythonにおけるログランク検定・一般化Wilcoxon検定
Pythonにおける生存時間解析はlifelinesモジュールにまとめられており、ログランク検定や一般化Wilcoxon検定はlifelines.statisticsモジュールのlogrank_test関数を用いて行うことができます。上記の説明の通りログランク検定と一般化Wilcoxon検定は統計量の重みづけが違うだけなので、logrank_test関数のweightings引数を変えるだけでログランク検定か一般化Wilcoxon検定かを区別することができます。
以下ではその方法を見ていきましょう。
サンプルデータ
ここではサンプルデータとして、喉頭癌のステージ別・年齢別の生存期間を表すデータセットを用いて、喉頭癌のStage IIとStage IVとで生存確率関数に有意差があるのかどうかを検定してみましょう。lifelinesモジュールのload_larynx関数を用いてサンプルデータを取得できます。
from lifelines import datasets
larynx_data = datasets.load_larynx()
print(larynx_data)

time age death Stage_II Stage_III Stage_IV 0 0.6 77 1 0 0 0 1 1.3 53 1 0 0 0 2 2.4 45 1 0 0 0 3 2.5 57 0 0 0 0 4 3.2 58 1 0 0 0 .. ... ... ... ... ... ... 85 2.3 62 1 0 0 1 86 2.9 74 0 0 0 1 87 3.6 71 1 0 0 1 88 3.8 84 1 0 0 1 89 4.3 48 0 0 0 1 [90 rows x 6 columns]
このうち、Stage IIとStage IVのデータを抽出してみます。
larynx_data_stage2 = larynx_data.query('Stage_II == 1')
larynx_data_stage4 = larynx_data.query('Stage_IV == 1')
ログランク検定を行う
先ほど取得したデータを用いてログランク検定を行ってみましょう。lifelines.statisticsモジュールのlogrank_test関数に検定する2つの生存期間とイベント発生の有無を指定することでログランク検定を行うことができます。
from lifelines.statistics import logrank_test
logrank_result = logrank_test(larynx_data_stage2.time, larynx_data_stage4.time, larynx_data_stage2.death, larynx_data_stage4.death)
print(logrank_result)
<lifelines.StatisticalResult: logrank_test>
t_0 = -1
null_distribution = chi squared
degrees_of_freedom = 1
test_name = logrank_test
---
test_statistic p -log2(p)
11.55 <0.005 10.52
これによりp値は0.005以下であり、喉頭癌のStage IIとStage IVの生存期間には有意差があることが分かりました。
一般化Wilcoxon検定を行う
続いて同じデータで一般化Wilcoxon検定を行ってみましょう。一般化Wilcoxon検定を行う場合は、logrank_test関数のweightings引数に’wilcoxon’を指定します。
from lifelines.statistics import logrank_test
wilcoxon_result = logrank_test(larynx_data_stage2.time, larynx_data_stage4.time, larynx_data_stage2.death, larynx_data_stage4.death, weightings='wilcoxon')
print(wilcoxon_result)
<lifelines.StatisticalResult: Wilcoxon_test>
t_0 = -1
null_distribution = chi squared
degrees_of_freedom = 1
test_name = Wilcoxon_test
---
test_statistic p -log2(p)
10.05 <0.005 9.36
先ほどと同様にp値は0.005以下であり、喉頭癌のStage IIとStage IVの生存期間には有意差があることが分かりました。
コードまとめ
最後にまとめとして、喉頭癌の生存期間のデータを読み込んでStage IIとStage IVとで生存確率関数に有意差があるか検定するコードを一連の流れでお示しします。
from lifelines import datasets
from lifelines.statistics import logrank_test
# データを読み込む
larynx_data = datasets.load_larynx()
larynx_data_stage2 = larynx_data.query('Stage_II == 1')
larynx_data_stage4 = larynx_data.query('Stage_IV == 1')
# ログランク検定を行う
logrank_result = logrank_test(larynx_data_stage2.time, larynx_data_stage4.time, larynx_data_stage2.death, larynx_data_stage4.death)
print(logrank_result)
# 一般化Wilcoxon検定を行う
wilcoxon_result = logrank_test(larynx_data_stage2.time, larynx_data_stage4.time, larynx_data_stage2.death, larynx_data_stage4.death, weightings='wilcoxon')
print(wilcoxon_result)










コメント