生存時間に関する回帰分析であるCox回帰分析は生存時間解析でよく用いられる手法です。Cox回帰分析を用いれば、複数の因子が生存に与える影響を解析したり、その寄与の大きさ(ハザード比)などを明らかにすることができます。
開発環境
- lifelines 0.26.3
- matplotlib 3.3.4
- Python 3.8.8

Cox回帰分析とは? ― 他の解析手法との違い
Cox回帰分析はイベントが発生するまでの期間を、複数の説明変数を用いてモデル化してその関係を解析する手法で、生存時間解析の1つです。医学統計でよく用いられるロジスティック回帰分析は「生存/死亡」のようにイベントが発生したか否かが目的変数となりますが、Cox回帰分析ではイベント発生するまでの期間が目的変数になる点に大きな違いがあります。
また、生存時間解析においてある要因の有無によって生存確率関数に差が出るかどうかを確かめる手法としてはログランク検定や一般化Wilcoxon検定が有名ですが、これらはある説明変数が結果に有意な影響を与えるかどうかを検定することはできますが、その影響の程度(ハザード比:生存(死亡)に何倍の影響があるか)を求めることはできません。そこで登場するのがCox回帰分析です。また、Cox回帰分析では連続量や複数の説明変数が生存に与える影響を検討することも可能となります。
Cox回帰分析の数学的背景
ハザード関数とCox回帰分析における仮定(比例ハザードモデル)
Cox回帰分析では比例ハザードモデルを仮定しているので、まずはこのことについて説明していきます。
ハザードとは、生存している標本におけるその瞬間の死亡確率のことを表し、一般化すると「まだイベントが発生していない標本におけるイベント発生確率」となります。以下では分かりやすくするために「イベント=死亡」の場合で説明します。
最初の標本数を基準としたときの累積死亡率\(D(t)\)は、生存関数\(S(t)\)を用いて\(D(t)=1-S(t)\)と表されます。ある瞬間\(t\)における死亡率は累積死亡率\(D(t)\)の時間微分となるので、
$$ \frac{d}{dt}D(t) = \frac{d}{dt}(1-S(t)) =- \frac{d}{dt}S(t) $$
となります(以下では、\(S(t)\)の時間微分を\(S'(t)\)とします)。ハザードは「生存している標本におけるその瞬間の死亡確率」であり、上記を時刻\(t\)における生存率\(S(t)\)で割ってハザード関数\(h(t) = – \displaystyle \frac{S'(t)}{S(t)} \)と表されます。
Cox回帰分析においては比例ハザード性と言って、次のように各々の群のハザード関数が比例関係にあると仮定したモデル(比例ハザードモデル)を考えます。基準となる生存関数\(S_0(t)\)のハザード関数(基準ハザード)を\(h_0(t)\)として、注目している生存関数\(S_1(t)\)のハザード関数を基準ハザードのr倍であるとします。この時、\(S_1(t)\)のハザード関数\(h_1(t)\)は
$$h_1(t) = r \cdot h_0(t)$$
となります。2群のハザード関数が比例関係にあるなら、その2つの関係は1つの比例定数\(r\)によって表すことができるので、特に基準ハザードとの比のことをハザード比と言います。
ハザード関数を用いて生存関数を表す
先ほどは、ハザード関数を生存関数を用いて表したので、今度は生存関数をハザード関数を用いて表してみましょう。
先ほど見たようにハザード\(h(t)\)と生存関数\(S(t)\)の関係は
$$ h(t) = – \displaystyle \frac{S'(t)}{S(t)} $$
ですが、これは
$$ \displaystyle S'(t) + h(t) \cdot S(t) = 0 $$
となり、これは一階線形同次微分方程式となるので、これを\(S(t)\)について解くと一般解は
$$ S(t) = C_0 \cdot e^{- \int h(t) dt} (C_0は積分定数)$$
となります。なお、この式のハザード関数の時間積分\(( \int h(t) dt )\)は累積ハザード関数\( H(t) \)と呼ばれています。
ここで\(t=0\)の時、累積ハザード関数は\(H(0)=0\)であり、生存関数は\(S(0)=1\)であることを考慮すると
$$ S(t) = e^{- \int h(t) dt}$$
となります。
ハザード関数の変化に対する生存関数の変化
比例ハザードモデルにおいては次のように基準ハザード\(h_0(t)\)の\(r\)倍であるハザード\(h_1(t)\)は次のように表せます。
$$h_1(t) = r \cdot h_0(t)$$
この時の生存関数\(S_1(t)\)は基準となる生存関数\(S_0(t)\)を用いて、
$$ S_1(t) = e^{- \int h_1(t) dt} = e^{- r \int h_0(t) dt} = (e^{- \int h_0(t) dt})^r = S_0(t)^r $$
と表せます。
Cox回帰分析
Cox回帰モデルでは先ほどの比例ハザード性の仮定に加えて、次の仮定も考えます。
注目している生存関数\(S_1(t)\)のハザード\(h_1(t)\)を基準ハザード\(h_0(t)\)の\(r\)倍であるとします。この時、Cox回帰モデルでは説明変数を\(x_1, x_2, x_3, …, x_n\)として、注目しているハザード関数の基準ハザードからの比(ハザード比)\(r\)を
$$r=e^{a_0 + a_1 \cdot x_1 + a_2 \cdot x_2 + a_3 \cdot x_3 + … + a_n \cdot x_n}$$
で表します。(対数線形性の仮定)
以上をまとめると、Cox回帰モデルでは
- 比例ハザード性の仮定:\(h_1(t) = r \cdot h_0(t)\)
- ハザード比の対数線形性の仮定:\(r=e^{a_0 + a_1 \cdot x_1 + a_2 \cdot x_2 + a_3 \cdot x_3 + … + a_n \cdot x_n}\)
が必要となります。
得られた生存関数(ハザード関数)をこの式に従って評価し、それぞれの回帰係数\( ( a_1, a_2, a_3, …, a_n ) \)の値や信頼区間を調べるのがCox回帰分析になります。
Cox回帰分析で算出される回帰係数とハザード比
Cox回帰分析では「因子Aのハザード比は2」などのように結果を得ることができますが、ここでいうハザード比とは「他の因子の値を0として、その因子Aの値だけ1にした時のハザード比」となります。
つまり、その因子Aの回帰係数を\(a_1\)とすると
$$r=e^{a_1}$$
がその因子Aのハザード比(HR)となります。
(その回帰係数自体はハザード比の対数 log(HR) に相当します)
比例ハザード性を満たす生存関数
比例ハザード性を満たす場合は、生存関数\(S_1(t)\)のハザード比を\(r\)とすると基準生存関数\(S_0(t)\)を用いて
$$ S_1(t) = S_0(t)^r $$
と表せます。
では、具体的にこの比例ハザード性を満たす関係とそうでない関係を見てみましょう。
比例ハザード性を満たす場合
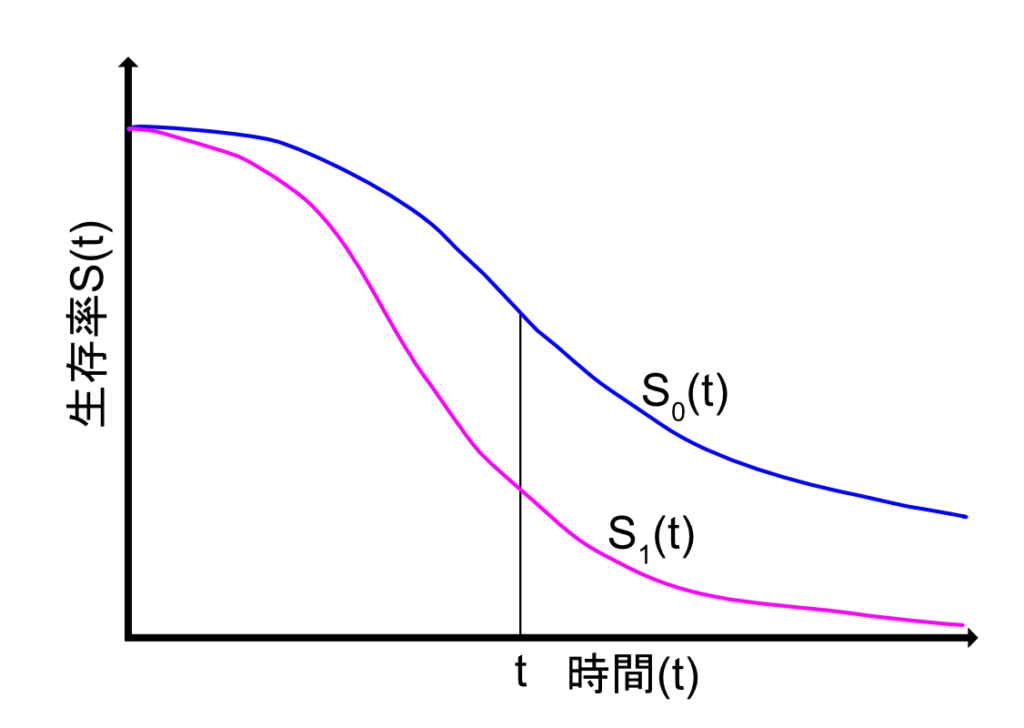
比例ハザード性を満たす場合は常に\( S_1(t) = S_0(t)^r \)の関係が成り立つので、\(S_1(t)\)と\(S_o(t)\)のグラフは交わることなく、その関係は一定となります。
比例ハザード性を満たさない場合
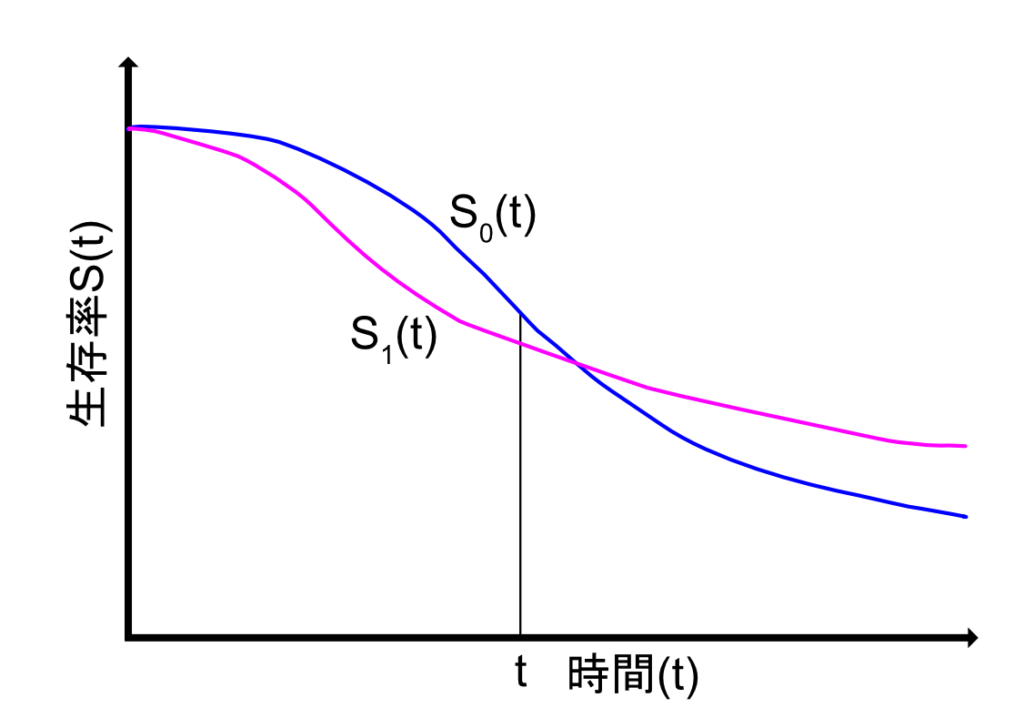
\(S_0(t)\)と\(S_1(t)\)の関係が一定ではないケースでは比例ハザード性を満たしているとは言えません。例えば、このグラフのように\(S_0(t)\)と\(S_1(t)\)が交わるような場合が相当します。
サンプルデータ
ここではサンプルデータとして、白血病に対するランダム化比較試験で検査値・治療と生存期間の関係を表したデータセットを用いて、検査値と治療が生存期間に対してどのように影響を与えるかをCox回帰分析で見てみましょう。lifelinesモジュールのload_leukemia関数を用いてサンプルデータを取得できます。
from lifelines import datasets
leukemia_data = datasets.load_leukemia()
print(leukemia_data.head())
t status sex logWBC Rx 0 35 0 1 1.45 0 1 34 0 1 1.47 0 2 32 0 1 2.20 0 3 32 0 1 2.53 0 4 25 0 1 1.78 0
このデータに関する説明はありませんが、おそらく
- t:生存期間
- status:生存(0)か死亡(1)か
- sex:性別
- logWBC:白血球数の対数値
- Rx:治療群(0)かプラセボ群(1)か
であると思われます。
※ 公式リファレンスには記載がありませんが、ここでは上記の通り解釈して説明を進めます。
Cox回帰分析を行う
先ほどのデータセットを用いてCox回帰分析を行ってみましょう。CoxPHFitterインスタンスを生成し、fitメソッドにデータセットと、そのデータセットにおける生存期間とイベントを表す項目名を指定してフィットさせます。print_summaryメソッドでフィットさせた結果を表示させてみましょう。
from lifelines import CoxPHFitter
cph = CoxPHFitter()
cph.fit(leukemia_data, duration_col='t', event_col='status')
cph.print_summary()
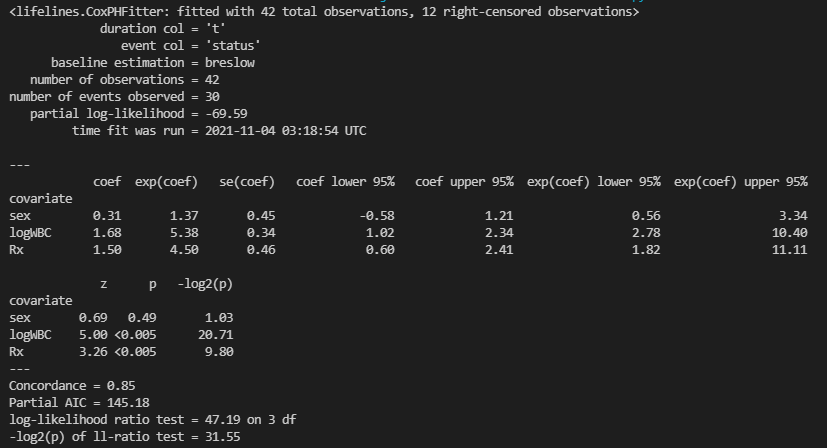
この結果からlogWBCとRxのp値が0.005以下と低く有意な因子であることが分かります。つまり、コントロール群では治療群よりも有意にハザードが高く、また白血球数が多いほど有意にハザードが高いという結果が得られました。両者の回帰係数(coef)はそれぞれ1.68と1.50であり、ハザード比(exp(coef))は5.38と4.50となっています。
なお、CoxPHFitterインスタンスはplotメソッドで簡単にそれぞれの項目のハザード比と信頼区間をグラフで表すことが可能です。
cph.plot()
plt.show()
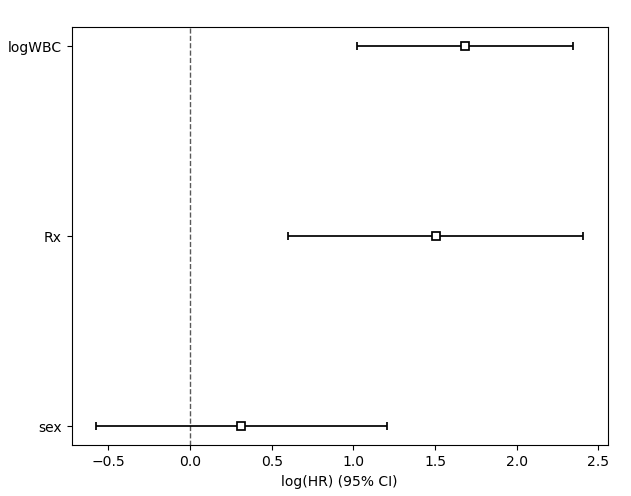
このグラフでもlogWBCとRxが有意であることが分かり、sexは予後に関係ないこともよく分かります。このグラフで出力されているのはハザード比の対数(log(HR))であり、回帰係数であることに注意してください。
コードまとめ
最後にまとめとして、データを読み込んでCox回帰分析を行う流れをお示しします。
from lifelines import datasets
from lifelines import CoxPHFitter
import matplotlib.pyplot as plt
# データの読み込み
leukemia_data = datasets.load_leukemia()
# Cox比例回帰モデルに当てはめる
cph = CoxPHFitter()
cph.fit(leukemia_data, duration_col='t', event_col='status')
cph.print_summary()
# グラフ化する
cph.plot()
plt.show()








コメント