2つの項目について観測した度数分布を考えたときに、その2つの項目に相関関係があるのかどうかを度数分布をもとに独立性の検定を用いて統計学的に検定することができます。
ここでは、その2つの分布が独立(=無関係)かどうかを検定する独立性の検定について見ていき、Pythonを用いた実装方法を説明します。

開発環境
- Python 3.7.9
- scipy 1.6.0
\(\chi^2\)検定を用いた独立性の検定の数学的背景
n個のサンプルを観察したときに、それぞれのサンプルについての項目①「1, 2, 3」と項目②「A, B, C」の観察された個数を表した以下のような表を分割表と呼びます。
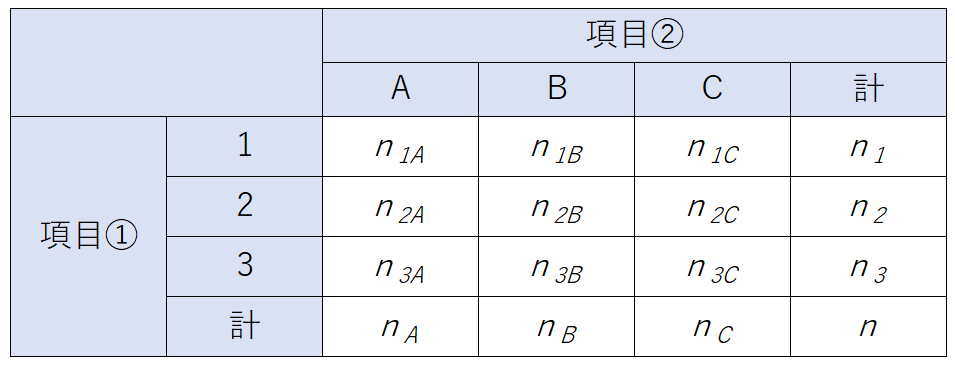
例えばn2Bは観察したサンプルのうちで、項目①については「2」で、なおかつ項目②に関しては「B」であるものの個数を表しています。この時、項目①と項目②とが独立であるなら、例えば項目①が「2」で項目②が「B」となる確率 \(p(2\cap B)\) については独立事象の乗法定理から、
$$p(2\cap B)=p(2) \cdot p(B)$$
となります。同様にして、観察したサンプルのすべての場合について、項目①と項目②とが独立である場合の理論確率は次のように求めることができます。
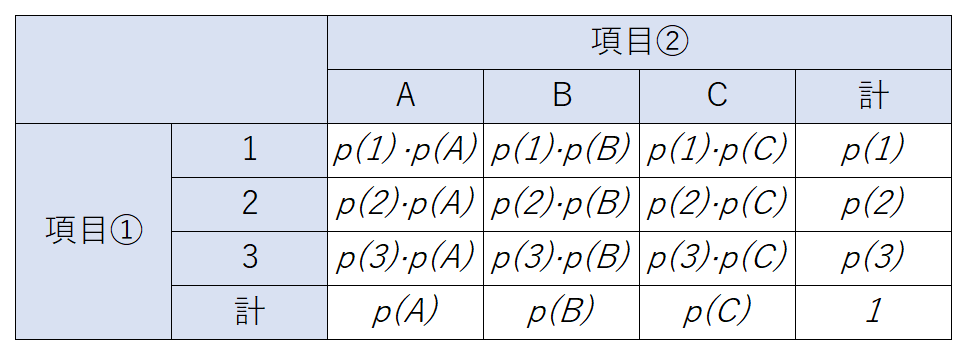
ここで、p(A)は項目②がAであるものの個数\(n_A(=n_{1A}+n_{2A}+n_{3A})\)を用いて以下のように表せます。
$$p(A)=n_A / n$$
つまり、以上より分割表のすべての欄について、観測度数と理論確率とが求まったことになるので、理論確率にサンプル数をかけることで期待度数を求めることが可能です。そして、観測度数と理論度数・期待度数を求めることができれば、独立性の検定は「『項目①と項目②が独立である』という仮定の下での期待度数に観測度数が適合しているかどうか」の適合度検定に置き換えて考えることができます。適合度検定については以下の記事をご覧ください。なお、適合度検定では\(\chi^2\)分布を用いますが、\(R \times C\)分割表の場合はその自由度は\( (R-1) \times (C-1)\)となります。
ここで適合度検定におけるピアソンの適合度基準は標本数が十分大きい時には\(\chi^2\)分布に従うと近似できますが、標本数が小さいと誤差が大きくなるので注意が必要です。特に標本数が少ない\(2 \times 2\)分割表についての独立性の検定では、\(\chi^2\)検定よりもFisherの直接確率検定の方が正確とされており、値が10以下のセルがあるときはFisherの直接確率検定の使用を考慮します。
具体的な例
具体的な例をもとに独立性の検定を行ってみましょう。ある大学の学生400人の物理と数学の成績が以下の通りだったとします。
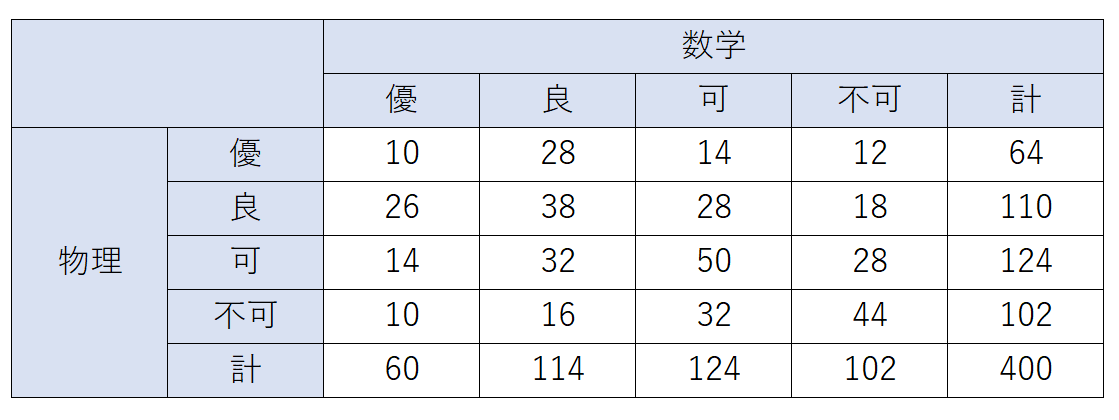
この時、物理の成績と数学の成績は独立であると言えるでしょうか?それとも「数学の成績が良い人は物理の成績もよい」などの何らかの関係があるでしょうか?
独立性の検定を行う
それでは、先ほどの物理と数学の成績の例について、独立性の検定を用いてその成績に関連があるかどうかを有意水準5%で検定してみましょう。この時の帰無仮説と対立仮説は次のようになります。
- 帰無仮説:物理の成績と数学の成績は独立している
- 対立仮説:物理の成績と数学の成績は独立ではない(≒何らかの相関関係がある)
この検定を手計算で行う場合は、まず分割表の一つ一つの欄について以下のように物理と数学の成績が独立である場合のそれぞれの理論確率を求める必要があります。
$$例:p(物理=良 \cap 数学=良)=p(物理=良) \cdot p(数学=良)$$
その上で、実際の観測度数がこの理論確率から求められた期待度数と適合するかどうかを、適合度の検定と同様の方法で確かめます(自由度は\(3 \times 3\))。
しかし、実際にこれをやってみるとかなりの手間になってしまうので、Pythonでは分割表を指定するだけで自動的に独立性の検定を行ってくれる関数が用意されています。scipy.statsモジュールのchi2_contingency関数の引数に分割表をnumpy.ndarrayオブジェクトとして指定するだけで次のように独立性の検定を行ってくれます。
import numpy as np
from scipy import stats
contingency_table = np.array([[10, 28, 14, 12], [26, 38, 28, 18], [14, 132, 50, 28], [10, 16, 32, 44]])
result = stats.chi2_contingency(contingency_table)
print(result)
(88.83089715155876, 2.793346838082888e-15, 9, array([[ 7.68 , 27.392, 15.872, 13.056],
[13.2 , 47.08 , 27.28 , 22.44 ],
[26.88 , 95.872, 55.552, 45.696],
[12.24 , 43.656, 25.296, 20.808]]))
chi2_contingency関数の戻り値は順番に、「\(\chi^2\)統計量」「\(p\)値」「自由度」「期待度数を表す分割表」となります。

今回の例では\(p\)値は2番目の戻り値の2.7933…x10-15となり、仮に帰無仮説が真であるとすると今回の観測度数と同じか、より極端な観測度数が偶然得られる確率は2.7933…x10-15であるという意味になります。ここでは最初に有意水準を5%としているので、「その確率が5%以下であるならば、それは偶然ではない(=有意である)」とあらかじめ設定しています。帰無仮説が真であるときに今回の観測度数が偶然得られる確率は2.7933…x10-15であり0.05(5%)よりも小さいことから、これは偶然ではない(=有意である)ということになり、帰無仮説は棄却されます。つまり、今回の観測度数は独立である場合の理論確率に従っておらず独立ではないと言えます。
以上より、物理の成績と数学の成績には何らかの関係があるということが分かりました。









コメント