実験の測定データにはばらつきが生じてしまいますが、測定ミスや何らかの外部的な要因でどう考えてもおかしい値が出ることがあります。しかし、そのようなデータを明確な基準もなく除外してしまっては、恣意的なデータとなってしまい、データの信頼性を落とす結果となってしまいます。もちろん、断りなくデータを除外してしまってはデータの改ざんになってしまいます。
そのようなときに、外れ値を統計的に判定する方法を持っていれば、1つの基準として使えますよね。ここでは、外れ値を統計学的に判定する方法を説明していきます。

四分位範囲を用いた簡易的な外れ値の検出法
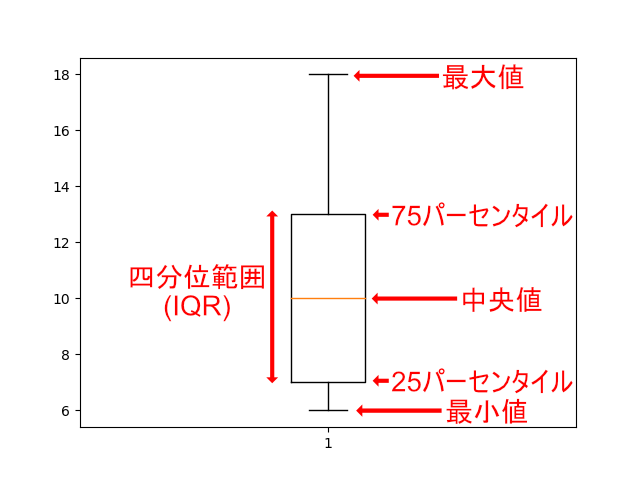
測定データを箱ひげ図でプロットしたときの箱の大きさが四分位範囲(IQR)になり、「第3四分位点(75パーセンタイル) – 第1四分位点(25パーセンタイル)」で定義されています。
箱ひげ図については以下の記事もご覧ください。

この四分位範囲を用いて、簡易的に以下の範囲を外れ値として判定することができます。
- (第1四分位点) – 1.5 x IQR より小さい値
- (第3四分位点) + 1.5 x IQR より大きい値
ここで示すように、IQRから±IQR x 1.5の範囲の外を外れ値とすることが多いですが、この外れ値の範囲は任意の値で設定することができます。ただし、恣意的な値にならないように注意が必要です。
Smirnov-Grubbs検定を用いた外れ値の検出法
Smirnov-Grubbs検定について
Smirnov-Grubbs検定(スミルノフ・グラブス検定)とは、データが正規分布に従うときに、測定されたデータの外れ値を検出する方法です。
まず、次のような帰無仮説と対立仮説を立てます。
- 帰無仮説: 全てのデータは同じ母集団からのものである。
- 対立仮説: 測定されたデータのうち、最大(最小)のものは外れ値である。
測定されたデータのうち、平均値から最も外れているデータ(最大値もしくは最小値)が、他の測定データと同じ正規分布に従っているかを検定し、帰無仮説が棄却された場合にそのデータを外れ値とします。次にそのデータを除外した上で、もう一度平均値から最も外れているデータ(最大値もしくは最小値)が、他の測定データと同じ正規分布に従っているかを検定します。この操作を外れ値が出なくなるまで繰り返すのがSmirnov-Grubbs検定です。
測定されたデータの標本平均を\( \bar x\)、不偏分散を\(U\)とすると、測定データ\( x_i \)に対して標準化した統計量\(T_i\)は
$$T_i=\frac{ \vert x_i – \bar{x} \vert}{\sqrt{U}}$$
となります。
ここで、Smirnov-Grubbs検定の対立仮説は検定するデータによって「最大のものは外れ値である」もしくは「最小のものは外れ値である」になりますが、この場合は検定している時点でそのデータが正規分布のどちら側に外れているかは明らかであるので、片側検定を行います。
統計量\(T_i\)の値がSmirnov-Grubbs検定の有意点の値よりも大きければ帰無仮説を棄却し、検定しているデータは外れ値であると判断されます。
- スミルノフ・グラブス検定の有意点 (外部サイト)
Smirnov-Grubbs検定を実行してみる
Smirnov-Grubbs検定はRのoutliersパッケージのgrubbs.test関数で実装されています。
また、Pythonでの実装は以下のサイトで公開されています(この実装は両側検定です)。
まとめ・参考サイト
外れ値検出法はここに示したもの以外にも多く考案されています。しかし、いずれの場合も外れ値と判定されたからといってそれを安易に棄却するのではなく、外れ値が生じた原因を突き止めることを怠ってはいけません。
なお、外れ値検出に関しては以下のサイトの情報が有用であり、参考にさせていただきました。








コメント