アフィン変換【OpenCV】

2021-09-132021-09-19

アフィン変換(1次変換)を用いると、図形を平行移動、拡大縮小、回転、せん断変形することができます。ここではOpenCVを用いてアフィン変換を行う方法を見ていきましょう。

開発環境

OpenCV 4.2.0
Python 3.7.9

[toc]

アフィン変換とは？
アフィン変換を行う
合成変換を行う
スポンサーリンク

アフィン変換とは？

アフィン変換を用いると図形の平行移動、拡大縮小、回転・せん断変換を表現することができます。変換前の座標を(x, y)とすると、変換行列を$A$として変換後の座標(X, Y)は

$$\begin{pmatrix}X \\ Y \\ 1 \end{pmatrix} = A \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

と表せます。なお、変換行列は3×3の行列となります。また、Aという移動(変形)をしてからBという移動(変形)を行うというような場合は、変換行列を$BA$と表すことができます(合成変換)。

ここではアフィン変換の詳細についての説明は省きますので、アフィン変換については以下のサイトなどをご覧ください。

イメージングソリューション

アフィン変換（平行移動、拡大縮小、回転、スキュー行列）

アフィン変換を行う

OpenCVでアフィン変換を行う際にはwarpAffine関数を用います。warpAffine関数の第1引数に変換を行う画像を指定し、第2引数で変換行列を、第3引数で変換後の出力する画像のサイズを指定します。ここで、通常は変換行列は3×3行列ですが、その3行目は常に同じであることから、warpAffine関数では3行目を省略して2×3行列で変換行列を指定します。

なお、以下の例では C:\BioTech-Lab\lena.jpg という画像ファイルを読み込んで用います。

平行移動

x軸方向にdx、y軸方向にdyだけ平行移動するときのアフィン変換は

$$ \begin{pmatrix}X \\ Y \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 &dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

で表されます。OpenCVでは変換行列の3行目は省いて2×3行列で指定すればよいので、変換行列Mは次のように表せます。

9	`M` `=` `np.array([[1,` `0, dx], [0,` `1, dy]], dtype=float)`

これを用いて平行移動を行ってみましょう。ここではx軸方向・y軸方向のそれぞれに100ピクセルずつ移動しています。

import cv2
import numpy as np
 
img = cv2.imread(r'C:\BioTech-Lab\lena.jpg')
h, w = img.shape[:2]
 
dx = 100
dy = 100
M = np.array([[1, 0, dx], [0, 1, dy]], dtype=float)
img_warped = cv2.warpAffine(img, M, (w, h))
 
cv2.imshow('img',img_warped)
cv2.waitKey(0)
cv2.destroyAllWindows()

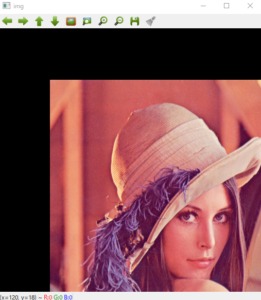
拡大・縮小

x軸方向にSx倍、y軸方向にSy倍するときのアフィン変換は

$$ \begin{pmatrix}X \\ Y \\ 1 \end{pmatrix} = \begin{pmatrix} Sx & 0 &0 \\ 0 & Sy & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

で表されます。OpenCVでは変換行列の3行目は省いて2×3行列で指定すればよいので、変換行列Mは次のように表せます。

9	`M` `=` `np.array([[Sx,` `0,` `0], [0, Sy,` `0]], dtype=float)`

これを用いて拡大・縮小を行ってみましょう。ここではx軸方向に0.5倍・y軸方向に0.8倍してみます。

import cv2
import numpy as np
 
img = cv2.imread(r'C:\BioTech-Lab\lena.jpg')
h, w = img.shape[:2]
 
Sx = 0.5
Sy = 0.8
M = np.array([[Sx, 0, 0], [0, Sy, 0]], dtype=float)
img_warped = cv2.warpAffine(img, M, (w, h))
 
cv2.imshow('img',img_warped)
cv2.waitKey(0)
cv2.destroyAllWindows()

回転

原点を中心に反時計回りにθ回転するときのアフィン変換は

$$ \begin{pmatrix}X \\ Y \\ 1 \end{pmatrix} = \begin{pmatrix} cosθ & -sinθ & 0 \\ sinθ & cosθ & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

で表されます。ただし、OpenCVの場合は左上が原点なので画像の中心で回転しようとすると平行移動と組み合わせる必要があり複雑な変換行列となってしまうので、変換行列を生成するためのgetRotationMatrix2D関数が用意されています。第1引数に回転中心の座標を、第2引数に回転角を弧度法で指定し、第3引数にスケールを指定します。

画像の中心で30°回転させる場合は次のようにします。

import cv2
import numpy as np
 
img = cv2.imread(r'C:\BioTech-Lab\lena.jpg')
h, w = img.shape[:2]
 
M = cv2.getRotationMatrix2D((int(w/2), int(h/2)), 30, 1)
img_warped = cv2.warpAffine(img, M, (w, h))
 
cv2.imshow('img',img_warped)
cv2.waitKey(0)
cv2.destroyAllWindows()

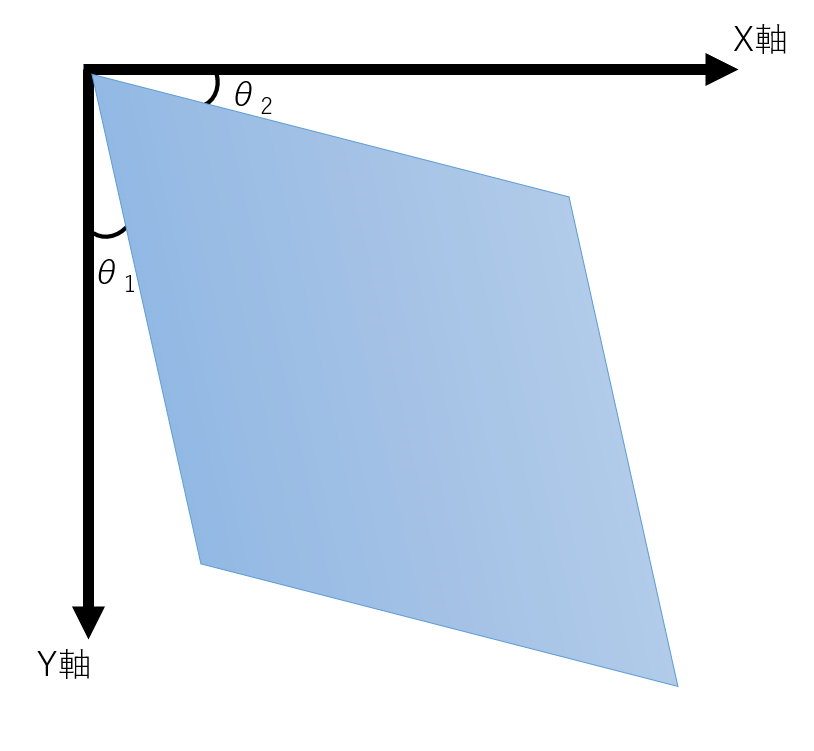
せん断

四角形の画像を平行四辺形に変形する処理をせん断と言います。$θ_1$をY軸からX軸への傾き、$θ_2$をX軸からY軸への傾き

$$ \begin{pmatrix} X \\ Y \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & tanθ_1 &0 \\ tanθ_2 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} $$

OpenCVでは変換行列の3行目は省いて2×3行列で指定すればよいので、変換行列Mはそれぞれ次のように表せます。

1	`M` `=` `np.array([[1, np.tan(theta1),` `0], [np.tan(theta2),` `1,` `0]], dtype=float)`

これを用いてせん断変形を行ってみましょう。y軸から30°変形させます($θ_1$=30)。

import cv2
import numpy as np
 
img = cv2.imread(r'C:\BioTech-Lab\lena.jpg')
h, w = img.shape[:2]
 
theta = np.deg2rad(30)
M = np.array([[1, np.tan(theta), 0], [0, 1, 0]], dtype=float)
img_warped = cv2.warpAffine(img, M, (int(1.5*w), h))
 
cv2.imshow('img',img_warped)
cv2.waitKey(0)
cv2.destroyAllWindows()

ここで、NumPyの三角関数は弧度法ではなくラジアンなので7行目で変換しています。また、OpenCVではx軸は画像の上側で、y軸は下向きなので、変換結果は次のようになります。

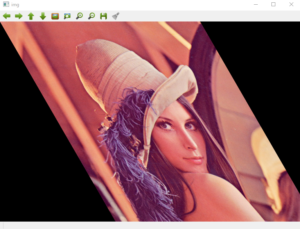
合成変換を行う

変換行列$A$と$B$について、$A$という移動(変形)をしてから$B$という移動(変形)を行うというような場合を合成変換と呼び、変換行列を$BA$と表すことができます。しかし、OpenCVにおけるアフィン変換では通常の3×3行列ではなくて2×3行列で変換行列を表しているので、そのまま行列の積を計算することができません。そこで、合成変換を行えるように変換行列の積を計算する関数を作成してみましょう。

import cv2
import numpy as np
 
def composite(M1, M2):
    M1_tmp = np.array([M1[0], M1[1], [0,0,1]])
    M2_tmp = np.array([M2[0], M2[1], [0,0,1]])
    M_tmp = np.dot(M1_tmp, M2_tmp)
    M = np.array([M_tmp[0], M_tmp[1]])
    return M
 
img = cv2.imread(r'C:\BioTech-Lab\lena.jpg')
h, w = img.shape[:2]
 
# 平行移動 
dx = 100
dy = 100
M1 = np.array([[1, 0, dx], [0, 1, dy]], dtype=float)
 
# 回転移動
M2 = cv2.getRotationMatrix2D((int(w/2), int(h/2)), 30, 1)
 
# 変換行列の合成
M = composite(M1, M2)
 
img_warped = cv2.warpAffine(img, M, (w, h))
  
cv2.imshow('img',img_warped)
cv2.waitKey(0)
cv2.destroyAllWindows()