目次
多角形の描画
多角形を1つ描画する
polylines関数を用いて、画像・頂点のリスト・閉じた図形かどうか・色を指定することで多角形を描画します。頂点の組み合わせは(頂点数 x 2)のndarrayで表し、pts引数にリストとして渡します。
import numpy as np
import cv2
img = np.zeros((300, 300, 3), np.uint8)
points = np.array([(50, 50), (100, 50), (250, 200), (180, 250)])
cv2.polylines(img, [points], True, (255, 255, 0))
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
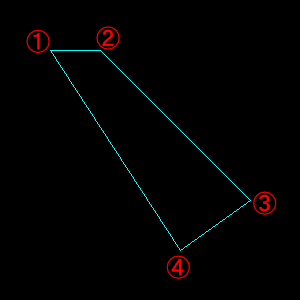
ここで指定した頂点の順番に線をつないでいきます。上の例の③と④を入れ替えると次のようになります。
import numpy as np
import cv2
img = np.zeros((300, 300, 3), np.uint8)
points = np.array([(50, 50), (100, 50), (180, 250), (250, 200)])
cv2.polylines(img, [points], True, (255, 255, 0))
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
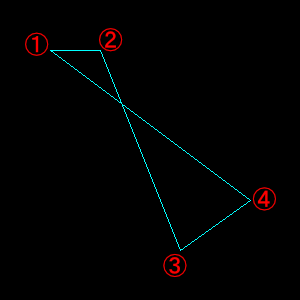
多角形を複数描画する
複数の多角形を一度に描画する場合は、頂点の一覧を表すndarrayを多角形の数だけ作成し、リストとしてpolylines関数のpts引数に指定します。
import numpy as np
import cv2
img = np.zeros((300, 300, 3), np.uint8)
pts1 = np.array([(50, 50), (100, 50), (250, 200), (180, 250)])
pts2 = np.array([(50, 100), (100, 200), (50, 250)])
cv2.polylines(img, [pts1, pts2], True, (255, 255, 0))
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

内部が塗りつぶされた多角形を描画する
多角形を1つ描画する
描画する多角形が1つのみの場合はfillPoly関数よりもfillConvexPoly関数の方が高速なので、fillConvexPoly関数を用います。fillConvexPoly関数では、points引数に頂点の一覧を表すndarrayをそのまま渡すだけで描画可能です。
import numpy as np
import cv2
img = np.zeros((300, 300, 3), np.uint8)
points = np.array([(50, 50), (100, 50), (250, 200), (180, 250)])
cv2.fillConvexPoly(img, points, (255, 255, 0))
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

多角形を複数描画する
複数の多角形をまとめて描画する場合はfillPoly関数を用います。pts引数に頂点の一覧を表すndarrayを多角形の数だけリストとして渡します。
import numpy as np
import cv2
img = np.zeros((300, 300, 3), np.uint8)
pts1 = np.array([(50, 50), (100, 50), (250, 200), (180, 250)])
pts2 = np.array([(50, 100), (100, 200), (50, 250)])
cv2.fillPoly(img, [pts1, pts2], (255, 255, 0))
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

RotatedRectを描画する
OpenCVではRotatedRectオブジェクトを描画する関数が、なぜか用意されていません。RotatedRectに内接する楕円はellipse関数で描画できるのですが…
そこで、RotatedRectを描画するには、それぞれの頂点の座標を求めてpolylines関数を用います。
import numpy as np
import math
import cv2
def rotatedRectangle(img, rotatedRect, color, thickness=1, lineType=cv2.LINE_8, shift=0):
(x,y), (width, height), angle = rotatedRect
angle = math.radians(angle)
# 回転する前の矩形の頂点
pt1_1 = (int(x + width / 2), int(y + height / 2))
pt2_1 = (int(x + width / 2), int(y - height / 2))
pt3_1 = (int(x - width / 2), int(y - height / 2))
pt4_1 = (int(x - width / 2), int(y + height / 2))
# 変換行列
t = np.array([[np.cos(angle), -np.sin(angle), x-x*np.cos(angle)+y*np.sin(angle)],
[np.sin(angle), np.cos(angle), y-x*np.sin(angle)-y*np.cos(angle)],
[0, 0, 1]])
tmp_pt1_1 = np.array([[pt1_1[0]], [pt1_1[1]], [1]])
tmp_pt1_2 = np.dot(t, tmp_pt1_1)
pt1_2 = (int(tmp_pt1_2[0][0]), int(tmp_pt1_2[1][0]))
tmp_pt2_1 = np.array([[pt2_1[0]], [pt2_1[1]], [1]])
tmp_pt2_2 = np.dot(t, tmp_pt2_1)
pt2_2 = (int(tmp_pt2_2[0][0]), int(tmp_pt2_2[1][0]))
tmp_pt3_1 = np.array([[pt3_1[0]], [pt3_1[1]], [1]])
tmp_pt3_2 = np.dot(t, tmp_pt3_1)
pt3_2 = (int(tmp_pt3_2[0][0]), int(tmp_pt3_2[1][0]))
tmp_pt4_1 = np.array([[pt4_1[0]], [pt4_1[1]], [1]])
tmp_pt4_2 = np.dot(t, tmp_pt4_1)
pt4_2 = (int(tmp_pt4_2[0][0]), int(tmp_pt4_2[1][0]))
points = np.array([pt1_2, pt2_2, pt3_2, pt4_2])
cv2.polylines(img, [points], True, color, thickness, lineType, shift)
return img
img = np.zeros((300, 300, 3), np.uint8)
rotatedRect = ((150, 150), (200, 120), 20)
rotatedRectangle(img, rotatedRect, (255, 255, 0))
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

折れ線の描画
polylines関数のisClosed引数をFalseに設定することで、始点と終点が閉じずに折れ線になります。
import numpy as np
import cv2
img = np.zeros((300, 300, 3), np.uint8)
points = np.array([(50, 50), (100, 50), (250, 200), (180, 250)])
cv2.polylines(img, [points], False, (255, 255, 0))
cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()









コメント